Problem Description

In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space. These characters divide the square into contiguous regions.

(Note that backslash characters are escaped, so a \ is represented as "\\".)

Return the number of regions.

Example 1

Input:

[ " /",
  "/ " ]

Output: 2

Explanation: The 2x2 grid is as follows:

Example 2

Input:

[ " /",
  "   " ]

Output: 1

Explanation: The 2x2 grid is as follows:

Example 3

Input:

[ "//",
  "/ " ]

Output: 3

Explanation: The 2x2 grid is as follows:

Intuition

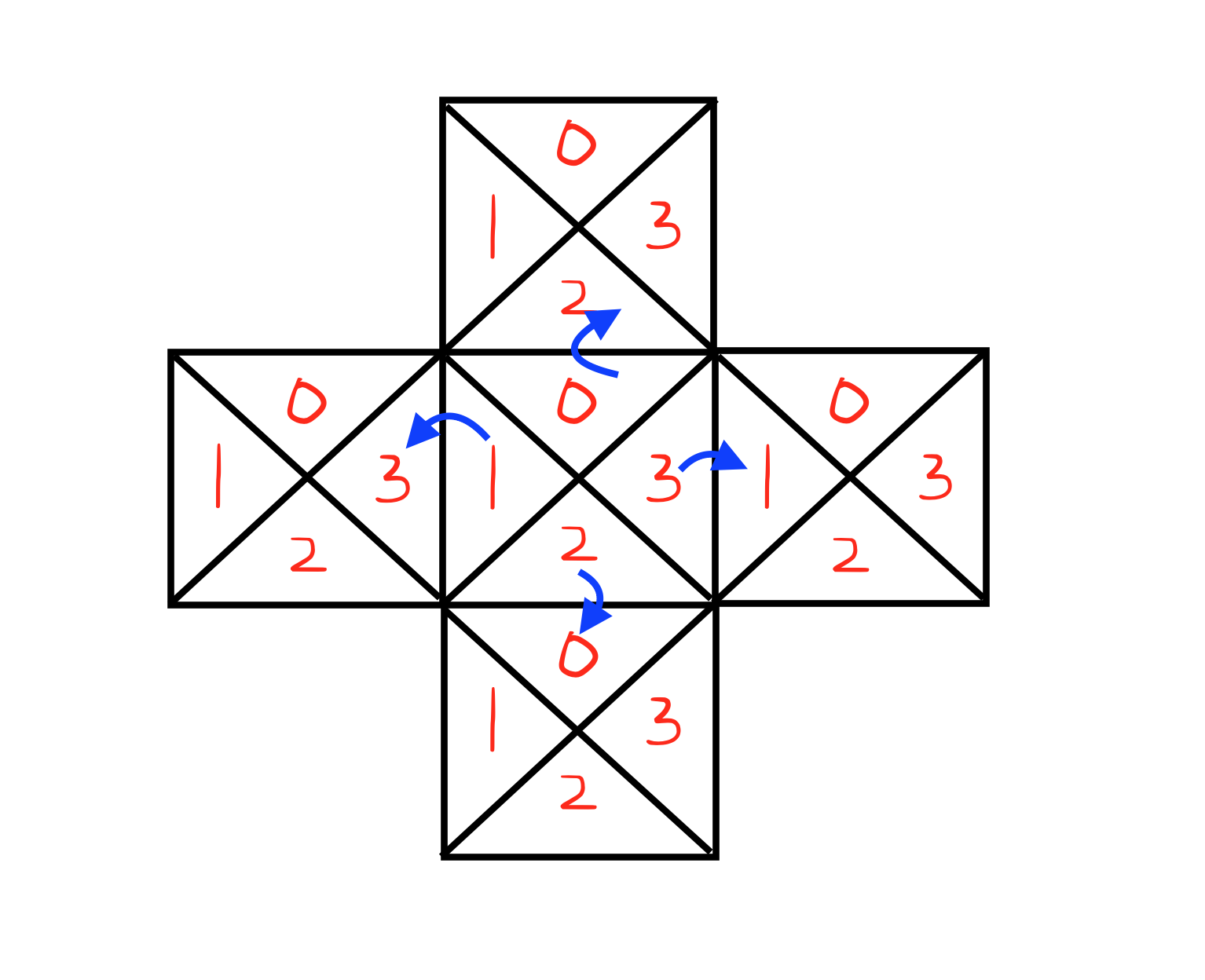
To find the number of components in a graph, we can use either depth-first search or union find. To use Union find, we must find independent units that we can union each other later to form a component. A cell of the input grid could be our base unit but with more careful inspection, it’s actually not. A cell will be split if the character in the cell is a \ or / but we can divide a cell into smaller scale like this.

This kind of intuition comes from the drawing and tests. Each grid cell is associated with four triangles(north, south, west, and east). You can see even with both front slash and back slash present these trianfles can’t be split into units in a smaller scale. Thus, these triangles should be our base units for solving this problem by using Union Find.

Algorithm

Create a 4*N*N nodes, one for each grid cell, represents a triangle and connect them if they are contiguous. After we use a Union Find structure to find the number of connected components.

Solution

class DSU:
    def __init__(self, N):
        self.parent = [i for i in range(N)]

    def find(self, x):
        if self.parent[x] != x:
            self.parent[x] = self.find(self.parent[x])
        return self.parent[x]

    def union(self, i, j):
        p = self.find(i)
        q = self.find(j)
        self.parent[p] = q

class Solution:
    def regionsBySlashes(self, grid):
        """
        :type grid: List[str]
        :rtype: int
        """
        N = len(grid)
        dsu = DSU(4 * N * N)

        for i in range(N):
            for j in range(N):
                idx = i * N + j
                # '0' -> North, '1' -> West, '2' -> South, '3'  -> 'East'
                if grid[i][j] == ' ':
                    dsu.union(4 * idx + 0, 4 * idx + 1)
                    dsu.union(4 * idx + 0, 4 * idx + 2)
                    dsu.union(4 * idx + 0, 4 * idx + 3)
                elif grid[i][j] == '\\':
                    dsu.union(4 * idx + 0, 4 * idx + 3)
                    dsu.union(4 * idx + 1, 4 * idx + 2)
                else:
                    dsu.union(4 * idx + 0, 4 * idx + 1)
                    dsu.union(4 * idx + 2, 4 * idx + 3)

                if i != 0:
                    dsu.union(4 * idx + 0, 4 * (idx - N) + 2)
                if i != N - 1:
                    dsu.union(4 * idx + 2, 4 * (idx + N) + 0)
                if j != 0:
                    dsu.union(4 * idx + 1, 4 * (idx - 1) + 3)
                if j != N - 1:
                    dsu.union(4 * idx + 3, 4 * (idx + 1) + 1)

        s = set([dsu.find(x) for x in range(4 * N *   N)])
        return len(s)

Complexity Analysis

Time Complexity

For union part, each square grid has at most 7 union operations. Thus the total time complexity for all union operations should be O(N*N) where N is the length of the grid. When counting the number of connected components in the graph, we find parent for each of the triangle which should be at most O(N). The time complexity of all find operations should be at most O(4*N*N*N). We only use path compression in the union find. If we add rank with it, the time cost can be reduced to O(N∗N∗α(N)), α is the Inverse-Ackermann function.

Space Complexity

O(N*N)